| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Gausian Density Estimation
- SQL 데이터 분석 첫걸음
- Digital Pathology
- PM4Py
- Tomek links
- OCSVM
- Grad-CAM
- GAN
- Inatance segmentation
- XAI
- 거리 기반 이상탐지
- Generative modeling
- Petri net
- Data Imbalance
- Condensed neares neighbor rule
- Sequence data
- Text generation
- 밀도 기반 이상탐지
- multi modal
- 딥러닝
- Process Mining
- auto encoder
- One-Sided Selection
- Clustering 기반 이상탐지
- 국비지원교육
- Random Undersampling
- 프로세스 마이닝
- Meta heuristic
- Fixed Learning
- 병리 AI
- Today
- Total
Create Opportunities
[알고리즘] Hash, Greedy, Sort 본문
어떤 자료구조를 택하느냐에 따라서 적용 가능한 알고리즘이 달라진다.
1. 완주하지 못한 선수 (Hash)
Hash 특징을 살펴보자.
- 이름 대신에 번호가 주어졌다면? → 선형 배열 (인덱스로 몇 번째 원소에 접근 가능하다.)
- 배열의 인덱스 말고 문자열로 접근할 수 있는 좋은 자료구조는 뭐가 있을까? → Hash!!!
- 문자열을 key로 보고 hash table에 mapping 시킬 수 있는 자료구조.
- 각각의 key값은 hash function으로 mapping 가능.
- hash bucket이 많을수록 다른 버킷에 사상될 가능성이 높아질 것임.
- 같은 버킷에 들어가면 충돌이 일어남.
Python의 dictionary를 생각해볼 수 있다.
dictionary를 구현할 때 내부적으로 Hash table을 이용하기 때문에 사전의 원소들을 해시를 이용해 O(1)에 접근 가능하다.
temp dictionary를 만들고 → get()로 모든 원소를 담는다. → 완주한 선수들은 -1 적용
내 풀이
# 참가자 / 완주자
# 완주하지 못한 선수들의 이름을 return
def solution(participant, completion):
answer = []
for i in range(len(participant)):
if participant[i] not in completion:
answer.append(participant[i])
else:
completion.remove(participant[i])
return ''.join(answer)왜 틀렸는가
- 동명이인 고려하지 않았다. 이후에 동명이인 고려해서 풀어도 봤지만, 시간 복잡도 고려하지 않았다. 어떤 자료구조로 접근할 수 있을지 우선적으로 생각하자.
강사 풀이

def solution(participant, completion):
d = {}
# 아래의 for문 시간 복잡도는 participant 길이에 비례
for x in participant:
d[x] = d.get(x, 0) + 1 # 처음 등장하면 1
# 아래의 for문 시간 복잡도는 completion 길이에 비례
for x in completion:
d[x] -= 1
# list comprehension -> 사전의 크기에 비례하는 시간 복잡도
dnf = [k for k, v in d.items() if v > 0] # value가 0보다 큰 key값 담음.
answer = dnf[0]
return answer
# 결과적으로 시간 복잡도는 n에 비례하는 linear time 복잡도.
2. 체육복 (Greedy)
Greedy 문제
- 알고리즘의 각 단계에서 그 순간 최적이라고 생각하는 것을 선택한다.
- 탐욕법으로 최적해를 찾을 수 있는 문제는 현재의 선택이 마지막 해답의 최적성을 해치지 않는 경우가 해당된다. (= 지금 좋은게 끝에도 좋다.)
- 탐욕법 적용 가능성을 어떻게 확인하냐? → 빌려줄 학생을 정해진 순서로 살펴야 하고, 이 정해진 순서에 따라 우선하여 빌려줄 방향을 정해야 한다.
해당 문제에서 가장 분명한 방법을 봐보자.
착안점 : 학생 수는 기껏해야 30명.
학생 수만큼 배열을 확보하고, 여기에 각자가 가지고 있는 체육복 수를 기록한다. → 번호 순서대로 스캔하면서 빌려줄 관계를 정한다.
내 풀이
def solution(n, lost, reserve):
answer = n - len(lost)
for i in range(len(lost)):
if lost[i] in reserve:
lost.remove(lost[i])
reserve.remove(lost[i])
elif lost[i]+1 in reserve:
answer += 1
reserve.remove(lost[i]+1)
elif lost[i]-1 in reserve:
answer += 1
reserve.remove(lost[i]-1)
return answer왜 틀렸는가?
시간 복잡도 고려하지 않음.
Greedy로 접근해야겠다! 를 생각했으면, 그에 맞게 새로운 배열을 하나 만들어야 한다. 풀이는 바로 아래 코드와 같다.
내가 접근한 방식대로라면 추가 풀이로 푸는 것이 맞았다. set을 잘 활용했어야 한다. n이 상대적으로 너무 큰 경우에는 추가 풀이와 같은 방식으로 접근하는 것이 좋을 것이다.
강사 풀이
def solution(n, lost, reserve):
u = [1] * (n+2) # 모든 원소를 1로 초기화. 2개는 맨 앞, 뒤에 추가
for i in reserve: # 여벌 있는 인원 +1 -> O(n)
u[i] += 1
for i in lost: # 도난 -> O(n)
u[i] -= 1
for i in range(1, n+1): # 정확히 n회 반복 -> O(n)
if u[i-1] == 0 and u[i] == 2:
u[i-1:i+1]=[1,1]
elif u[i] == 2 and u[i+1] == 0:
u[i:i+2]=[1,1]
return len([x for x in u[1:-1] if x>0]) # O(n)여벌을 가져온 학생 처리 : reserve 길이에 비례
체육복 잃어버린 학생 처리 : lost 길이에 비례
체육복 빌려주기 처리 : 전체 학생 수 (n)에 비례
→ O(n) Linear time Algorithm
추가 풀이
set의 복잡도도 굳이 따져보면 O(n)임.
sort의 복잡도 : set(r)의 원소 수 = k -> klogk를 복잡도로 가짐.
def solution(n, lost, reserve):
s = set(lost) & set(reserve) # 교집합
l = set(lost) - s
r = set(reserve) - s
for x in sorted(r): # x = 체육복을 빌려줄 수 있는 학생 번호
if x-1 in l:
l.remove(x-1)
elif x+1 in l:
l.remove(x+1)
return n - len(l)3. 가장 큰 수 (Sort)
정렬 문제
sort()를 할 때 내가 정한 기준에 따라 배열을 정렬할 수 있어야 한다.
방법 1
- 빈 문자열로 수를 초기화한다.
- 가장 크게 만들 수 있는 수를 고른다.
- 그 수를 현재 수에 이어 붙이면서 계속 반복.
[3, 30, 34, 5, 9] → “” → “9” → “95” → “9534” → …
위 방법은 O(N^2) → 정렬 알고리즘을 사용해야 함.
방법 2
- 빈 문자열로 수를 초기화
- 수의 목록을 정렬 (크게 만드는 것을 우선으로) !! 오름차순, 내림차순 XXX
- 하나씩 꺼내서 이어 붙이면서 계속 반복.
O(NlogN)
크게 만드는 수의 기준은 그럼 뭔가?
Ex) 3 vs 32 → 332와 323을 비교 → 3이 와야함.
numbers.sort(key=lambda x:(x*4)[:4], reverse=True)
→ 내가 만든 기준을 적용하여 정렬하기 위함.
내 풀이
from itertools import permutations
def solution(numbers):
perm_list = list(permutations(numbers))
temp_list = []
for i in perm_list:
temp = ''.join(map(str,i))
temp_list.append(int(temp))
answer = str(max(temp_list))
return answer왜 틀렸는가?
permutations 함수로 numbers 배열의 모든 가능한 순열을 반환하므로 n!이된다. 그리고 for 문을 돌면서 각 순열의 문자열 결합, 정수 변환 및 temp_list에 추가하는 데 O(n)이 소요된다. 따라서 위 코드의 시간 복잡도는 O(n!*n)이다.
numbers의 크기가 증가할수록 시간복잡도는 기하급수적으로 증가하므로 정렬 알고리즘 사용을 고려할 수 있겠다.
강사 풀이
def solution(numbers):
numbers = [str(x) for x in numbers]
numbers.sort(key = lambda x : (x*4)[:4], reverse=True)
if numbers[0 == '0':
answer = '0'
else:
answer = ''.join(numbers)
return answer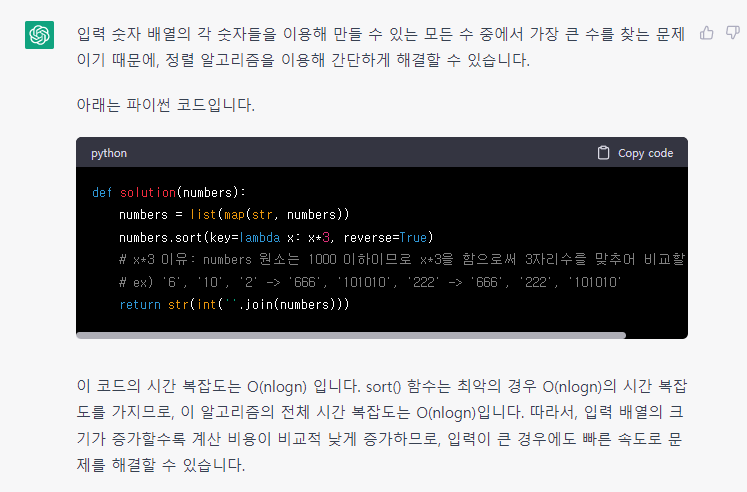
3. 큰 수 만들기 (Greedy)
Greedy 문제
- 앞 자리에 큰 수가 오는 것이 전체를 크게 만든다. → 따라서, 큰 것을 우선해서 골라 담고 싶다.
- 작은걸 빼되, 앞에서 빼야한다.
- 앞 자리에서부터 하나씩 골라서 담되, 지금 담으려는 것보다 작은 것들은 도로 뺀다. 단, k에 도달할 때까지만 반복한다.
- 큰 수가 앞 자리에, 작은 수가 뒷 자리에 놓이도록
- 이미 내림차순으로 정렬되어 있다면 ? → 뒤에부터 k만큼 지워야 함.

알고리즘 복잡도
- 가장 무식한 방법은 무엇인가. → 가능한 모든 조합의 수 (combinatorial explodure)
- 위에서 설계한 알고리즘의 복잡도는 ? → O(n) linear time algorithm
강사 풀이
def solution(number, k):
collected = []
for i, num in enumerate(number):
while len(collected) > 0 and collected[-1] < num and k > 0:
collected.pop()
k -= 1
if k == 0: # 다 뺐으면?
collected += list(number[i:])
break
collected.append(num)
collected = collected[:-k] if k > 0 else collected
answer = ''.join(collected)
return answercollected → 빈 리스트에 숫자를 모아서 큰 수를 만들기 위한 목적. 문자열은 immutable (불변하는) 특성을 가지고 있기 때문.
number를 순회하면서, 값의 인덱스와 값을 꺼낸다.
collected 리스트에 원소가 하나 이상 있고, 마지막 원소가 num보다 작고, k가 0보다 크면!!!
아래는 더 쉽게 풀어쓴 코드.
def solution(number, k):
answer = []
for num in number:
while k>0 and answer and answer[-1] < num: # k가 남아있고, answer에 값이 있고, answer 마지막 값이 이제 넣어야 할 값보다 작으면 진행.
answer.pop() # 마지막 값 빼자.
k -= 1 # k 하나 지움.
answer.append(num)
return ''.join(answer[:len(answer) - k])'알고리즘' 카테고리의 다른 글
| [알고리즘] Heap, Dynamic Programming, DFS/BFS (4) | 2023.04.09 |
|---|---|
| [알고리즘] 상담예약제, 티셔츠 (0) | 2023.03.16 |
| [알고리즘] 개인정보 수집 유효기간 (0) | 2023.03.07 |
| [알고리즘] 뒤에 있는 큰 수 찾기 (0) | 2023.03.06 |
| [알고리즘] 둘만의 암호 (1) | 2023.03.06 |



