| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- OCSVM
- Condensed neares neighbor rule
- Grad-CAM
- Generative modeling
- One-Sided Selection
- Petri net
- Text generation
- 국비지원교육
- Clustering 기반 이상탐지
- Process Mining
- 병리 AI
- Sequence data
- 프로세스 마이닝
- Fixed Learning
- Tomek links
- Digital Pathology
- 딥러닝
- 거리 기반 이상탐지
- GAN
- 밀도 기반 이상탐지
- XAI
- multi modal
- Data Imbalance
- PM4Py
- SQL 데이터 분석 첫걸음
- auto encoder
- Gausian Density Estimation
- Meta heuristic
- Random Undersampling
- Inatance segmentation
- Today
- Total
Create Opportunities
[ML] 차원 축소 알고리즘 본문
차원 축소
차원 축소 기법을 왜 배워야 하며, 왜 사용하는가?
- 수천, 수백만개의 feature를 가지고 ML/DL 학습을 진행하여 Y를 예측하게 된다. feature가 너무 많다면 학습이 느려질 뿐더러, 정확도 측면에서도 방해가 될 수 있다. (차원의 저주!!!)
- 우리는 3차원에 갇혀있다. 더 높은 차원을 볼 수 없다. 어떤 데이터가 왜 이상치인지 파악하기 위해서는 2,3차원 공간으로 축소해서 눈으로 확인해볼 수 있으며, 이에 기반한 이상탐지 기법이 다양하다.
차원 축소의 효과는?
- 변수 간 상관성을 제거할 수 있다.
- 학습 모델의 과적합을 방지할 수 있다.
- 학습 모델의 예측 성능의 향상을 유도할 수 있다.
- EDA에 활용될 수 있다.
차원 축소는 사실 큰 개념에서 보았을 때, 변수 선택 / 변수 추출로 나누어 볼 수 있다.
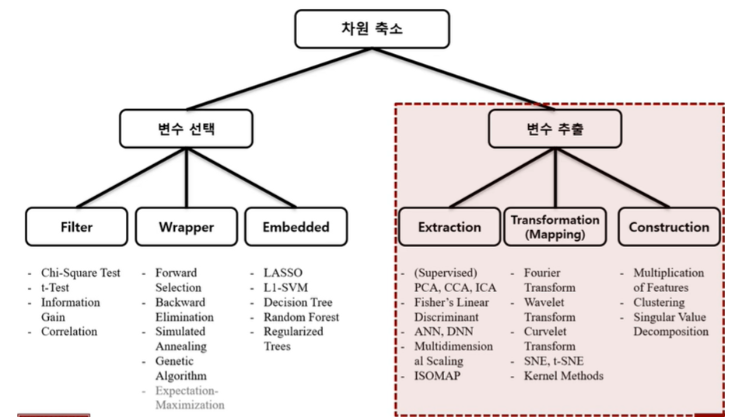
핸즈온 머신러닝에서는 변수 추출에 초점을 맞추어 설명하고 있다.
차원 축소 접근 방법 → (투영, 매니폴드)
- 투영
- 대표적인 알고리즘 PCA!!! 정의 : 직교선형 변환을 통하나 차원 축소 기법
핵심 개념은 선형 변환, 분산 보존, 주성분이다.
🐘 선형 변환이 왜 중요한데?
PCA 구축 과정이 선형 변환 그 자체라고 할 수 있다. 이는 주성분을 찾고 주성분이 이루는 Span에 투영하여 차원을 축소하는 과정이다.

🐘 분산 보존이 왜 핵심 개념이지?
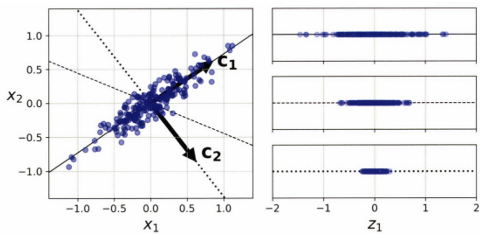
X 평면의 데이터를 Z 직선으로 투영 → 몇 번째가 가장 설명력 있는 차원축소인가?
확연하게 첫 번째이다. 왜? → 분산이 보존됐다.
왜 분산을 보존해야 하는가? → 정보 손실을 최소화 했기 때문이다.
분산 보존이 왜 정보 손실의 최소화인데? → MSE와 아래의 최적화 수식으로 설명 가능하다.

🐘 주성분을 어떻게 구하는데?
- 주성분 : 고유 분산을 최대한 보존하는 방향으로 변환하는 기저(축)
SVD를 통해 데이터를 decompose함으로써 주성분을 찾을 수 있는데…
https://angeloyeo.github.io/2019/08/01/SVD.html
특이값 분해(SVD) - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
전체 데이터(X)를 특이값 분해하면, X = UΣV^T 와 같이 표현할 수 있다.
- U는 직교 행렬로, 데이터의 행간의 관계를 나타내는 고유벡터로 구성된다.
- Σ는 대각행렬로, 고유값이 대각선으로 정렬된다. → 고유값 = 주성분이된다.
- V^T는 직교행렬로, 데이터의 열간의 관계를 나타내는 고유벡터로 구성된다.
🐘 PCA 구축 과정
Step1. 데이터 정규화 (평균을 0으로)
Step2. 공분산 행렬 계산
Step3. 고유값, 고유벡터 계산.
Random PCA : 빠르게 주성분을 찾아야 할 때. (주성분에 근사한 축을 찾음)
rnd_pca = PCA (n_components=154, svd_solver="randomized" )
X_ reduced = rnd_pca .fit_transform(X_train )Incremental PCA : 데이터가 너무 많을 때, 점진적으로 배치를 넣을 수 있다.
from sklearn.decomposition import IncrementalPCA
n batches = lØØ
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np .array_split(X_train, n_batches):
inc_pca .partial_fit(X_batch)
X_reduced = inc_pca .transform(X_train)Kernel PCA : rbf, sigmoid 커널을 활용한다면, 비선형 패턴을 고려할 수 있다. 지난주의 SVM 커널과 동일한 개념의 커널이다.
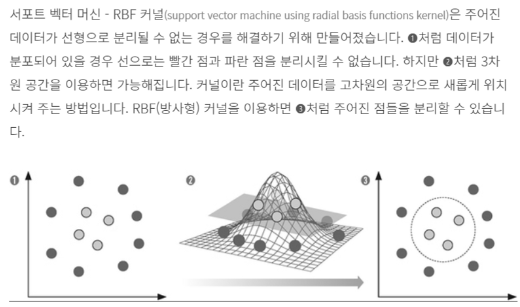
frαn sklearn.decomposition import KernelPCA
rbf_pca = KernelPCA(n_components = 2, kernel="rbf" , gallJl1a=Ø .04 )
X_reduced = rbf_pca .fit_transform(X)🐘 PCA의 한계점은?
데이터 변수 간 비선형적 패턴이 있는 경우 !!!
Non Gaussian distribution !!!
따라서 매니폴드 알고리즘이 존재한다.
🐘 LLE (locally linear embedding)
- 가장 가까운 이웃에 얼마나 선형적으로 연관되어 있는지 측정한다.
- 원 데이터 관계가 가장 잘 보존되는 차원을 찾는다.
- LLE는 노이즈가 많지 않은 경우 잘 작동한다.
🐘 LLE (locally linear embedding)
- 클래스 간 분리를 극대화하는 방식으로 동작한다.
- Classification Task에서 활용해볼 수 있겠다.
🐘 t-SNE
데이터들의 유사성을 유지하면서 저차원에서의 거리를 최대한 보존한다.
