| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- GAN
- multi modal
- 국비지원교육
- Generative modeling
- 프로세스 마이닝
- Fixed Learning
- Tomek links
- Grad-CAM
- Clustering 기반 이상탐지
- Gausian Density Estimation
- Inatance segmentation
- Meta heuristic
- Random Undersampling
- Data Imbalance
- 병리 AI
- 딥러닝
- 거리 기반 이상탐지
- Condensed neares neighbor rule
- One-Sided Selection
- Text generation
- XAI
- Petri net
- OCSVM
- Process Mining
- SQL 데이터 분석 첫걸음
- Sequence data
- Digital Pathology
- auto encoder
- 밀도 기반 이상탐지
- PM4Py
- Today
- Total
Create Opportunities
Meta Heuristics ? 본문
메타 휴리스틱이 무엇인가 천천히 알아보자.
자료구조를 공부하면 BFS, DFS를 배운다. 이들은, 최적을 보장하는 Exhaustive한 완전 탐색(Full-space search) 알고리즘이다. 이렇게 어떻게든 최적의 결과를 도출할 수 있는 알고리즘이 필요한 경우가 있겠지만, "효율"을 중시한다면? 더 빠르게 적당히 좋은 결과를 도출하고 끝내버리는게 좋을 수도 있겠다.

Heuristic이라는게 그거다. 근사 최적해. 즉 local optimal을 빠르게 찾고자 하는 방법이다. 휴리스틱이라 하면 "감"이라는 말이 떠오른다. 그냥 감으로 때려 맞추는 것도 휴리스틱이라고 할 수 있겠다.
휴리스틱 알고리즘에 해당되는 Greedy search 기법에는 최적해를 보장하는 알고리즘도 존재하긴 한다. Minimum Spanning Tree 문제 상황의 Kruscal 알고리즘이다.
Minimum Spanning Tree (MST)
이산수학에서의 그래프를 공부하면서 Spanning Tree를 배웠다. 모든 정점들이 연결되어 있어야 하고, 사이클을 포함해서는 안되기 때문에 n개의 정점을 정확히 n-1개의 Arc로 연결할 수 있어야 한다.
MST는 Arc에 가중치가 있으며, Tree의 가중합이 최소가 될 수 있도록 하는 Spanning Tree이다.
이러한 MST를 구현하기 위한 Krusckal 알고리즘은 컴퓨터 네트워크 교과목에서 배웠다. 이는 Greedy search에 해당되지만, 최적해를 보장한다. 아주 특이한 Case이다.
휴리스틱 알고리즘으로 해결할 수 있는 보통의 문제들은 아래와 같다. 이름을 들으면 예상할 수 있다.
Traveling Salesman Problem
Vehicle Routing Problem
Bin packing Problem
Metaheuristics (: A heuristic around heuristics)

그럼 Metaheuristics은 ???
쉽게 말해, 어떤 문제에도 범용적으로 쓰일 수 있는 휴리스틱 방법론이다. 위 그림이 의미하는 바는, 범용적인 Metaheuristic이 적용되는 상황에 추가적인 제약(Problem)이 추가된다면, 보통의 Heuristic 알고리즘이 된다는 것이다.

메타 휴리스틱의 특징은 아래와 같이 얘기해볼 수 있다.
1. 좋은 Process를 찾을 수 있는 전략을 제시할 수 있다.
2. 합리적인 시간 복잡도 내에서 suboptimal을 제공한다.
3. Global optimal은 보장하지 못한다.
4. Termination condition : 외부 요소, 반복 제한으로 인해 자주 중지된다.
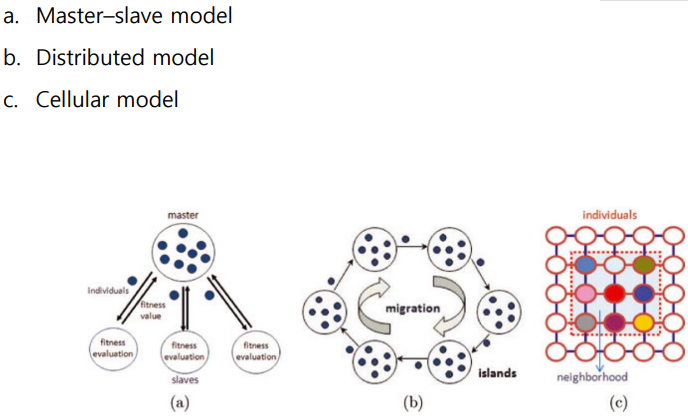
Parallel Metaheuristics

대부분의 메타 휴리스틱은 sequential하다. 대용량의 데이터를 처리하다보면, 시간 소모가 클 것이 분명하다.
간단하게만 생각해보더라도, 어떠한 알고리즘을 병렬 처리를 하여 근사 최적해를 도출하는 계산할 수 있다면, Search time을 줄여주고, 최적해의 질도 높여줄 수 있을 것이다.
Metaheuristics를 두 가지로 나누어 볼 수 있겠다.
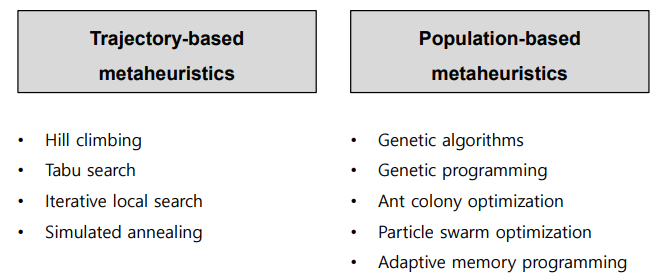
1) Trajectory-based metaheuristics
먼저 Trajectory based된 메타 휴리스틱 방법은 궤적 기반..으로 해석될 수 있을텐데, 쉽게 말해 점차적으로 local optimal에 근사해가는 방법이다.
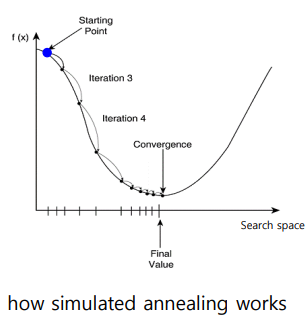
대표적으로 왼쪽의 Simulated annealing이 있다. 서서히 convex한 곳으로 이동하고 있는 것을 볼 수 있다.
또 이 Trajectory based 메타 휴리스틱에서 알고리즘의 종류를 나누어 본다면, 아래와 같다. 참고할 것.
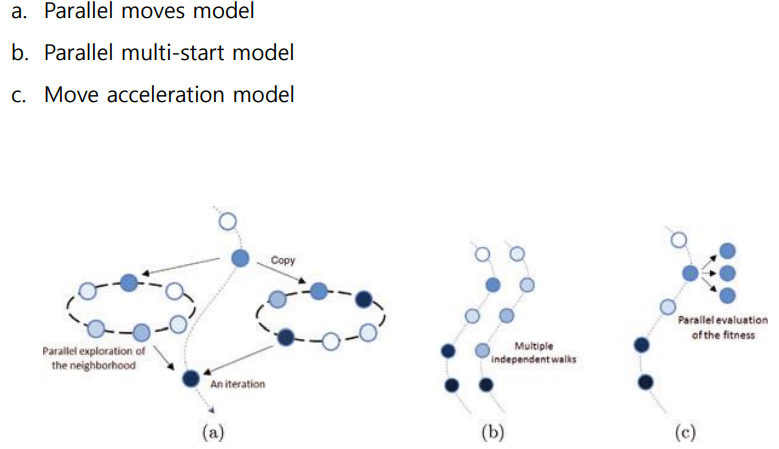
2) Population-based metaheuristics
다음으로 Population-based된 메타 휴리스틱 방법은 쉽게 말해 일단 여러개 던지고 보는거다. 던져놓고, 더 나은 값의 주변을 탐색하며 나아간다. 이렇게 점점 탐색의 범위를 좁혀가는 것이다. 아래의 그림을 보면 감이 온다. 이러한 알고리즘의 예로 Genetic Algorithm이 있다. 이 알고리즘은 참 널리 사용된다. Process Mining에서의 Discovery를 위한 알고리즘으로도 사용되는 것을 배웠다.
또 이 Population based 메타 휴리스틱에서 알고리즘의 종류를 나누어 본다면, 아래와 같다. 참고할 것.
추가로 작성할 내용은 너무너무 많은 것 같다.
'인공지능' 카테고리의 다른 글
| [인공지능 응용] eXplainable AI (SHAP) (0) | 2022.12.04 |
|---|---|
| [인공지능 응용] eXplainable AI (PDP, ICE, LIME) (0) | 2022.12.04 |
| [인공지능 응용] 데이터 불균형 문제 (3) (0) | 2022.10.04 |
| [인공지능 응용] 데이터 불균형 문제 (2) (1) | 2022.09.20 |
| [인공지능 응용] 데이터 불균형 문제 (1) (8) | 2022.09.19 |




